25 Survival analysis
All the aforementioned analysis deals with the presence or absence of an outcome. They do not take into consideration how long it took the outcome to occur. Survival analysis is designed for this purpose, analysis of time to events. For instance, analysing how long it takes for a car to develop a faulty engine, for a person to develop a heart attack and divorce after marriage will require survival analysis.
25.1 Terminologies
In survival analysis, subjects are usually followed for a period of time with our main interest being the duration it takes for the event to occur. To understand survival analysis we need to familiarise ourselves with a few terminologies. Consider Figure 42. At the beginning of the year 2001, a study was initiated to determine the survival of women treated for breast cancer. The six horizontal lines represent six patients recruited for this study and indicate their time of recruitment into the study, how long they were in the study and their outcome.
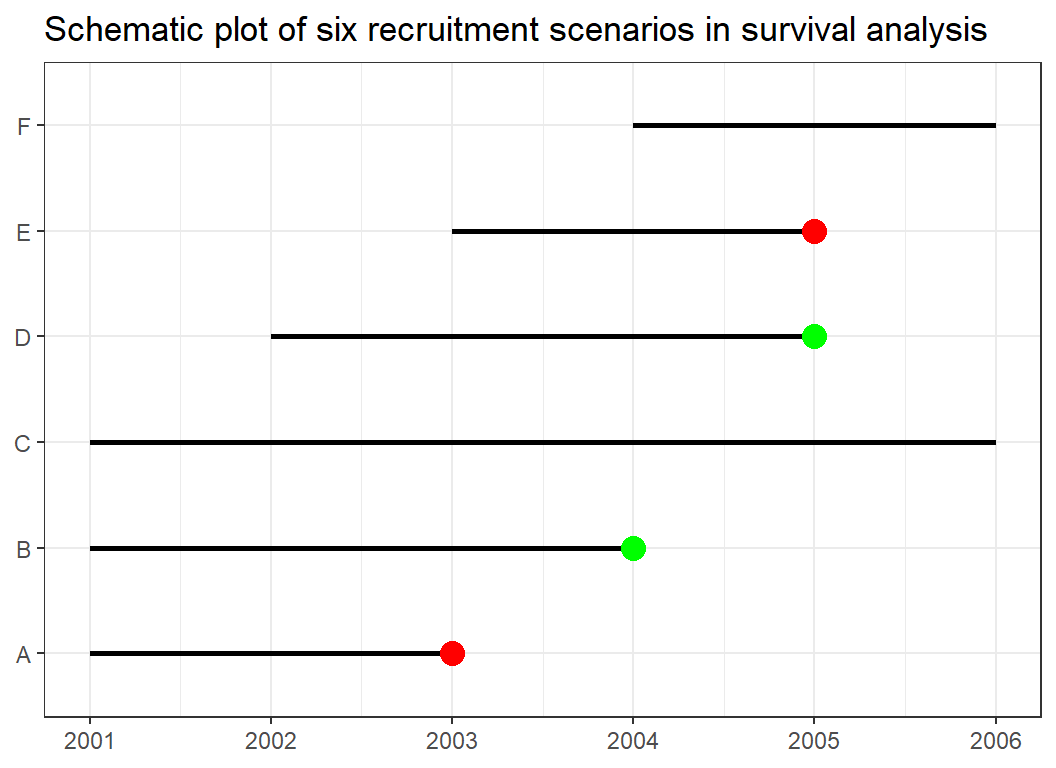
Survival: This is generally termed as the probability that an individual or a subject survives from the beginning of say a study or observation (where t0 = 0) to a specific time (t) without experiencing the event. So in a study where one is determining the survival of breast cancer patients, the five-year survival is the probability that a patient will be alive at five years after diagnosis or observation. This is also called the survival function and is often represented by S(t).
Hazard: The hazard on the other hand is the probability that an individual who has been under observation from time t0 has the event at time t. Relating this to our breast cancer example the hazard at five years is the probability that a patient would be dead at five years. The hazard function is often represented by or . Note that the survivor function deals with the event (death) not occurring while the hazard function deals with the event (death) occurring.
Event: The event we are interested in is death. In this example, death is the event of interest but this could be divorce, relapse of cancer, etc. depending on the outcome of the interest being studied. In our diagram, the event (death) is coloured red. Patient A was recruited in 2001 but died in 2003 while E was recruited into the study in 2003 but died in 2005. Hence both patients were in the study for about 2 years and experienced the event of death.
Censor: Patients who do not experience the event are usually said to be censored, literally meaning the time they will develop the event cannot be determined within the study period. Patient B for instance was recruited at the beginning of the study but lost to follow-up (green dot) in 2004. Patient D was recruited into the study in 2002 but was also lost to follow up in 2005. Patients C and F both stayed in the study till the end without experiencing the event. For patients B, C, D, and F we have no idea at the end of the the follow-up period when their events will occur. For these, their outcome is termed as censored. These six lines give us the characteristic scenarios that may occur in the right censored data.
Median Survival: It is the time when half the study subjects are expected to have experienced the event. In other words, the chance of surviving (or not experiencing the event) beyond that time is 50% for a population with the disease or exposure being studied.
In this section, we will use the lung data from the survival package. First, we have a look at the details of the lung data by using
| inst | time | status | age | sex | ph.ecog | ph.karno | pat.karno | meal.cal | wt.loss |
|---|---|---|---|---|---|---|---|---|---|
| 3 | 306 | 2 | 74 | 1 | 1 | 90 | 100 | 1175 | |
| 3 | 455 | 2 | 68 | 1 | 0 | 90 | 90 | 1225 | 15 |
| 3 | 1010 | 1 | 56 | 1 | 0 | 90 | 90 | 15 | |
| 5 | 210 | 2 | 57 | 1 | 1 | 90 | 60 | 1150 | 11 |
| 1 | 883 | 2 | 60 | 1 | 0 | 100 | 90 | 0 | |
| 12 | 1022 | 1 | 74 | 1 | 1 | 50 | 80 | 513 | 0 |
For a good understanding of the lung data readers are advised to read the help page revealed by the help() function above. Note that time is the duration each participant was followed up while in the study. status on the other hand indicates if the patient experienced the outcome, in this case, death while being followed up or was censored, indicating death never occurred during the follow-up period.
25.2 The survival object
The initial step in survival analysis in R (and for that matter many other statistical software) is the creation of the survival object. This is achieved in R with the function Surv() from the survival package. The function requires at least two arguments to be supplied. These include the time, indicating the duration each subject was in the study and status indicating whether the event occurred or not. This is demonstrated below using the “lung” dataset in the survival package.
Surv.1 <- Surv(time=lung$time, event=lung$status==2)
Surv.1
[1] 306 455 1010+ 210 883 1022+ 310 361 218 166 170 654
[13] 728 71 567 144 613 707 61 88 301 81 624 371
[25] 394 520 574 118 390 12 473 26 533 107 53 122
[37] 814 965+ 93 731 460 153 433 145 583 95 303 519
[49] 643 765 735 189 53 246 689 65 5 132 687 345
[61] 444 223 175 60 163 65 208 821+ 428 230 840+ 305
[73] 11 132 226 426 705 363 11 176 791 95 196+ 167
[85] 806+ 284 641 147 740+ 163
[ reached getOption("max.print") -- omitted 138 entries ]In the Surv()function above time is supplied as a numeric variable while the event is either expressed as 0 (for no event or censored) and 1 (for the event occurring) or FALSE (for no event or censoring) and TRUE (for the occurrence of the event). Our command above used the logical version (TRUE/FALSE) and created a vector of TRUE (for status of 2) and FALSE (for status otherwise).
The survival object is essentially a conversion of the time into an object that incorporates both the time and the status. Below we combine the time and status from the lung dataset and the survival object. It can be seen that the time variable is the same as the survival object if the patient died but in patients with censored outcomes, a plus (+) sign is attached.
cbind(lung[,2:3], Surv.1) %>% head()
Warning in value[[jj]][ri] <- if (is.factor(xij)) as.vector(xij) else xij:
number of items to replace is not a multiple of replacement length| time | status | Surv0.1 |
|---|---|---|
| 306 | 2 | 306 |
| 455 | 2 | 455 |
| 1010 | 1 | 1010 |
| 210 | 2 | 210 |
| 883 | 2 | 883 |
| 1022 | 1 | 1022 |
25.3 The survival fit object
Next, a survival object is created in accordance with the analysis intended to be done. The non-stratified analysis is currently fitted with a 1 on the right side of the formula as shown below while stratified survival is done with the stratifying variable on the right side of the formula.
In the analysis below we try to determine the median survival time for all persons included in the study
sfit.1 <- survfit(Surv.1 ~ 1)
sfit.1
Call: survfit(formula = Surv.1 ~ 1)
n events median 0.95LCL 0.95UCL
[1,] 228 165 310 285 363The survival fit object sfit.1 like a linear regression or logistic regression object has very little but important information at first hand. It shows the number of records used, the median survival time (the time at which it is expected that half the patients would have the event) and its confidence interval. Our analysis indicates that after 310 days half the patients would have died! The output is simple but there is more that can be revealed in the attributes. These are displayed below
25.4 Kaplan-Meier life table
For a compact view of these attributes, we summarise the survfit object. This is displayed below
summary(sfit.1)
Call: survfit(formula = Surv.1 ~ 1)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
5 228 1 0.9956 0.00438 0.9871 1.000
11 227 3 0.9825 0.00869 0.9656 1.000
12 224 1 0.9781 0.00970 0.9592 0.997
13 223 2 0.9693 0.01142 0.9472 0.992
15 221 1 0.9649 0.01219 0.9413 0.989
26 220 1 0.9605 0.01290 0.9356 0.986
30 219 1 0.9561 0.01356 0.9299 0.983
31 218 1 0.9518 0.01419 0.9243 0.980
53 217 2 0.9430 0.01536 0.9134 0.974
54 215 1 0.9386 0.01590 0.9079 0.970
59 214 1 0.9342 0.01642 0.9026 0.967
60 213 2 0.9254 0.01740 0.8920 0.960
[ reached getOption("max.print") -- omitted 127 rows ]The long table produced in this output is called the Kaplan-Meier life table. It contains the individual survival probabilities with their 95% confidence intervals at every point in time of the study. For instance, the proportion that survived to the end of day 30 is about 0.9561 (95%CI: 0.9299 to 0.983). The rather long life table can be significantly compacted to show only specific times. For instance, if we decide to show the survival in a life table for every 90 days we can specify these times below
summary(sfit.1, times=seq(0,900,90))
Call: survfit(formula = Surv.1 ~ 1)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0 228 0 1.0000 0.0000 1.0000 1.000
90 201 27 0.8816 0.0214 0.8406 0.925
180 160 36 0.7217 0.0298 0.6655 0.783
270 108 30 0.5753 0.0338 0.5128 0.645
360 70 24 0.4340 0.0358 0.3693 0.510
450 48 16 0.3287 0.0356 0.2659 0.406
540 33 10 0.2554 0.0344 0.1962 0.333
630 22 7 0.1958 0.0330 0.1407 0.272
720 14 8 0.1246 0.0290 0.0789 0.197
810 7 5 0.0783 0.0246 0.0423 0.145
900 3 2 0.0503 0.0228 0.0207 0.12325.5 Kaplan-Meier curve
The Kaplan-Meier life table can be plotted to give it a graphical representation called the Kaplan-Meier curve. The resulting curve is a plot of the Survival probability against the time. An example is shown in the figure below and plotted with
survminer::ggsurvplot(
sfit.1,
data = lung,
palette= 'blue',
surv.median.line = "hv",
censor =F,
title = "Kaplan-Meier Curve with 95% CI",
ggtheme = theme_bw())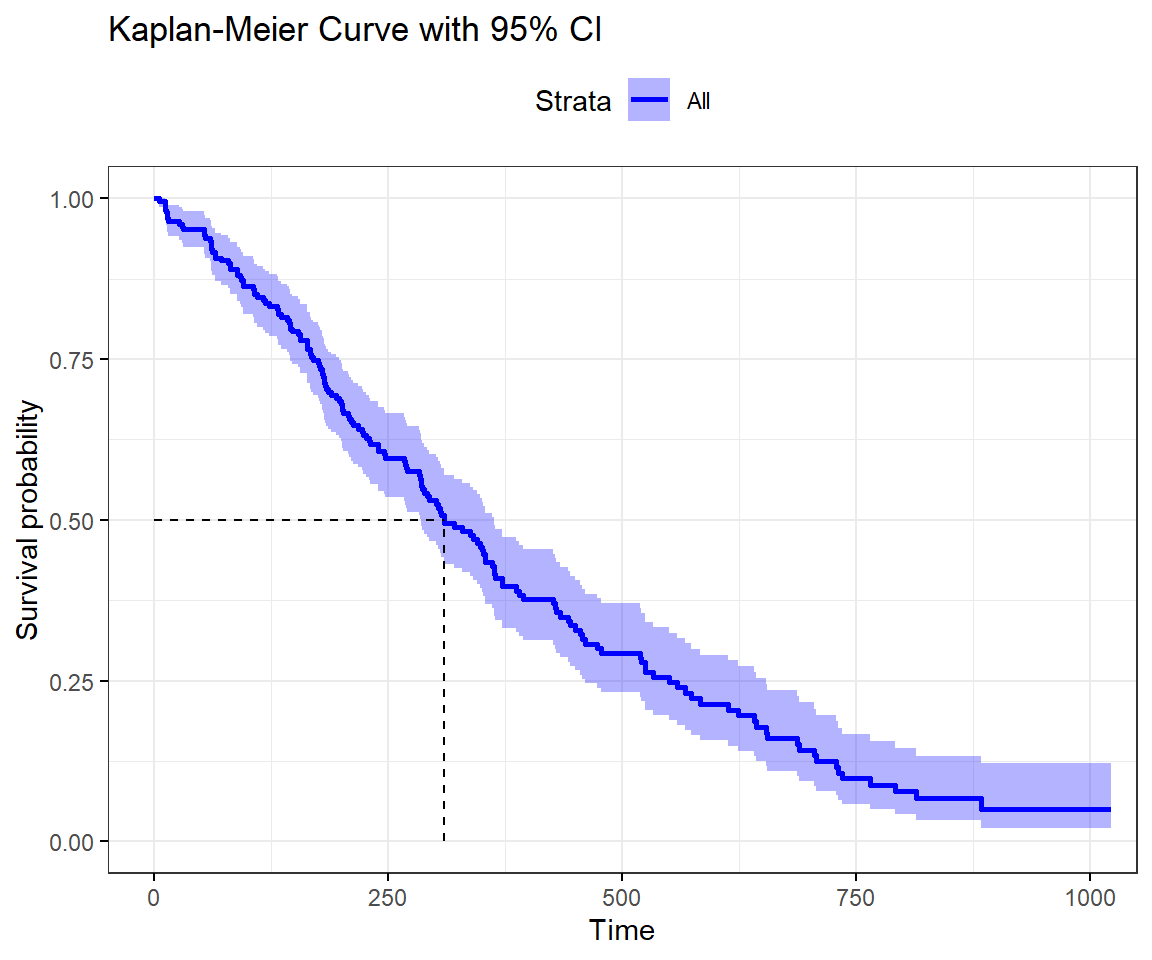
The green dotted line in the plot cuts the curve at the median survival time. Also, the plot has the confidence interval superimposed (dotted red lines).
25.6 Survival for subgroups
To determine the survival separately for subgroups we need to fit the survival object specifying our requisite group. For instance, to determine survival among the different sexes we fit the object as below. First, we make sure the sex variable is in the right format, a factor.
And then fit the appropriate survfit object. Note that the right-hand side of the formula this time is sex and not 1.
sfit.2 <- survfit(Surv.1 ~ lung$sex)
sfit.2
Call: survfit(formula = Surv.1 ~ lung$sex)
n events median 0.95LCL 0.95UCL
lung$sex=Male 138 112 270 212 310
lung$sex=Female 90 53 426 348 550Once again we are presented with the survfit object displaying the records, the number of events, the median survival and the confidence intervals. These statistics however are separate for each sex. For instance, we realise that the number of deaths in males was more than twice that for females and the median survival time for males of 270 days is lesser than that for females. As before, for a complete life table, we summarise the survfit object.
summary(sfit.2)
Call: survfit(formula = Surv.1 ~ lung$sex)
lung$sex=Male
time n.risk n.event survival std.err lower 95% CI upper 95% CI
11 138 3 0.9783 0.0124 0.9542 1.000
12 135 1 0.9710 0.0143 0.9434 0.999
13 134 2 0.9565 0.0174 0.9231 0.991
15 132 1 0.9493 0.0187 0.9134 0.987
26 131 1 0.9420 0.0199 0.9038 0.982
30 130 1 0.9348 0.0210 0.8945 0.977
31 129 1 0.9275 0.0221 0.8853 0.972
53 128 2 0.9130 0.0240 0.8672 0.961
54 126 1 0.9058 0.0249 0.8583 0.956
59 125 1 0.8986 0.0257 0.8496 0.950
60 124 1 0.8913 0.0265 0.8409 0.945
65 123 2 0.8768 0.0280 0.8237 0.933
[ reached getOption("max.print") -- omitted 87 rows ]
lung$sex=Female
time n.risk n.event survival std.err lower 95% CI upper 95% CI
5 90 1 0.9889 0.0110 0.9675 1.000
60 89 1 0.9778 0.0155 0.9478 1.000
61 88 1 0.9667 0.0189 0.9303 1.000
62 87 1 0.9556 0.0217 0.9139 0.999
79 86 1 0.9444 0.0241 0.8983 0.993
81 85 1 0.9333 0.0263 0.8832 0.986
95 83 1 0.9221 0.0283 0.8683 0.979
107 81 1 0.9107 0.0301 0.8535 0.972
122 80 1 0.8993 0.0318 0.8390 0.964
145 79 2 0.8766 0.0349 0.8108 0.948
153 77 1 0.8652 0.0362 0.7970 0.939
166 76 1 0.8538 0.0375 0.7834 0.931
[ reached getOption("max.print") -- omitted 39 rows ]The rather long life table can best be appreciated with a KM curve. We further go ahead to plot the Kaplan-Meier curve for the two sexes as shown in Figure 44 and plot with
plot(
sfit.2,
col=1:2,
lty=1:2,
mark.time=F,
main="K-M curve by sex",
xlab = "Days", ylab="Survival")
legend("topright", c("Male","Female"), lty=1:2, col=1:2)
abline(h=0.5, lty=2, col=3)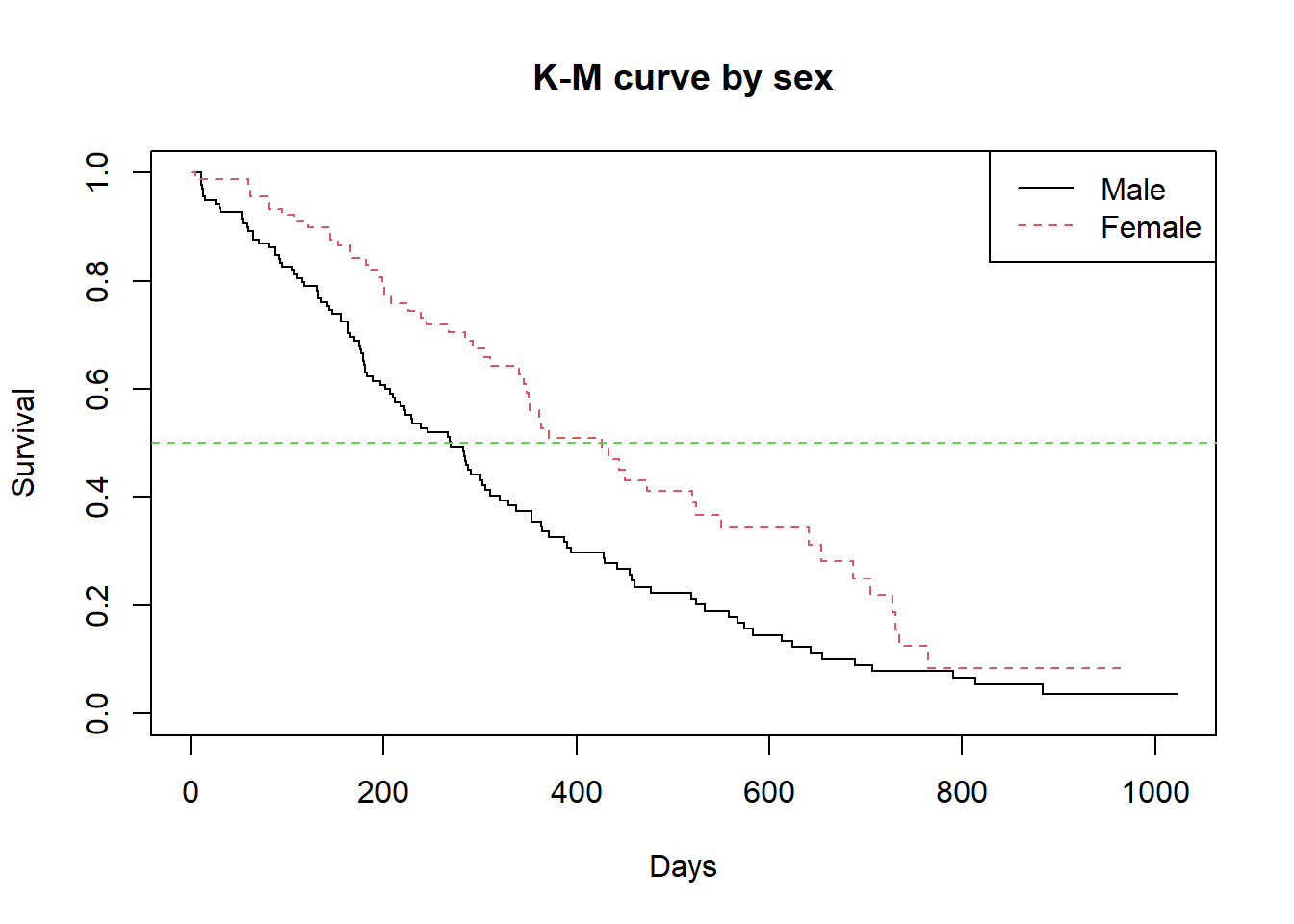
survminer::ggsurvplot(
sfit.2,
data = lung,
surv.median.line = "hv",
censor = F,
title = "Kaplan-Meier Curve by sex (with 95% CI)",
ggtheme = theme_bw(),
conf.int = T,
xlab = "Days")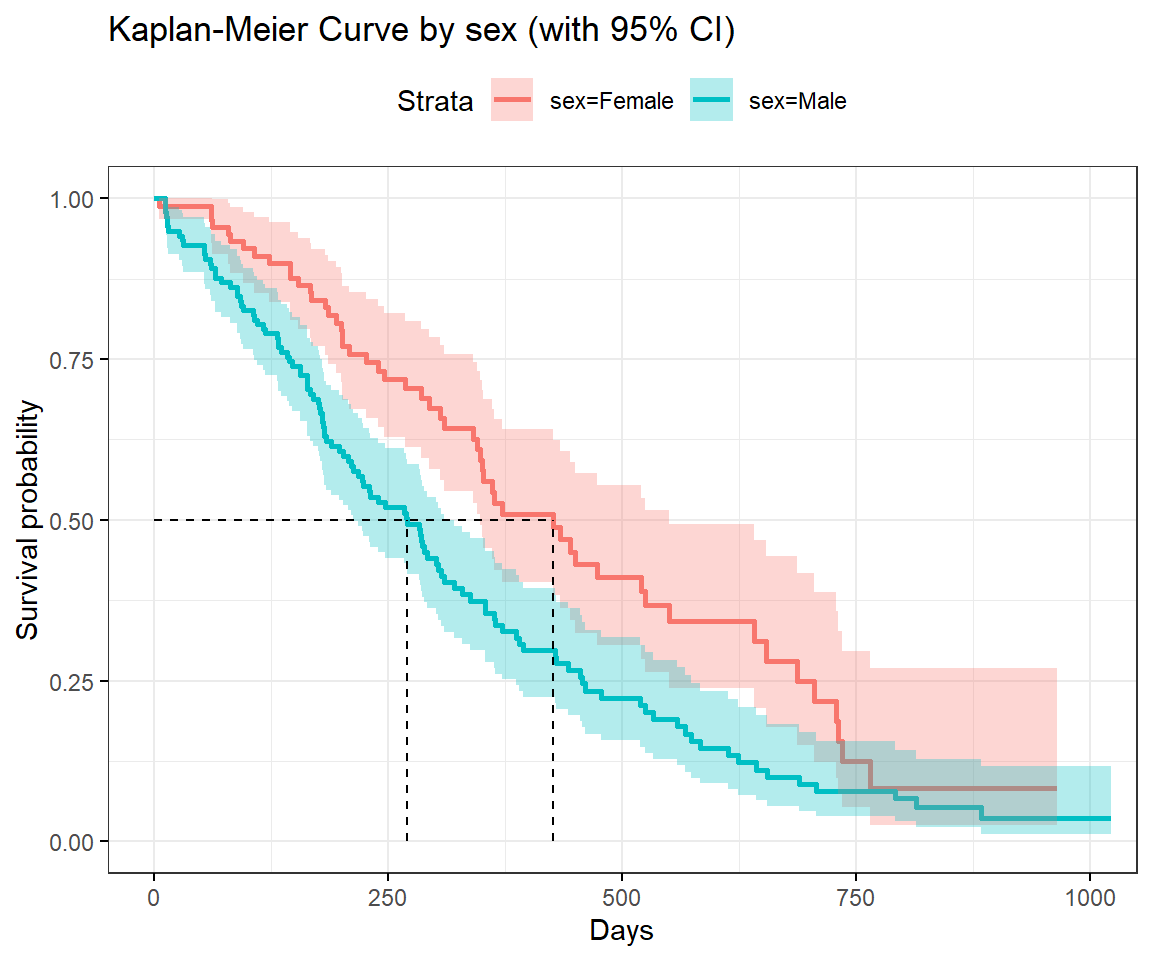
The figure above shows the KM survival curve separately for males and females. It can be seen that the two plots are completely separate, a sign that the survival is not the same in both sexes. The steeper curve for the males indicates they have a relatively worse outcome over time than the females. The median survival time for instance (indicated by the green dotted line) intersects the males’ curve much earlier than the females indicating a much lower median survival time for the males compared to the females.
25.7 Cumulative Incidence (Hazard)
Another way of expressing the relationship between time to an outcome and the outcome is with the Cumulative Incidence (CI). The CI at any point in time is a measure of the frequency of the outcome over a period of time. This can be determined in R as below. First, we fit the survival object.
sfit.3 <-
survfit(
Surv(
time = time,
event = status==2,
type = "mstate") ~ 1,
data=lung)
sfit.3
Call: survfit(formula = Surv(time = time, event = status == 2, type = "mstate") ~
1, data = lung)
n nevent rmean*
(s0) 228 0 376.2747
TRUE 228 165 645.7253
*restricted mean time in state (max time = 1022 )The survival object is similar to that done previously but this time in fitting it we used the argument type="mstate" to specify our preference for the cumulative incidence. We further use the summary() function on the survfit object to generate the CI table.
| time | n.risk | n.event | n.censor | estimate | std.error | conf.high | conf.low | state |
|---|---|---|---|---|---|---|---|---|
| 5 | 228 | 0 | 0 | 0.995614 | 0.00437634 | 1 | 0.987073 | (s0) |
| 11 | 227 | 0 | 0 | 0.982456 | 0.00869464 | 0.999646 | 0.965562 | (s0) |
| 12 | 224 | 0 | 0 | 0.97807 | 0.00969918 | 0.997266 | 0.959244 | (s0) |
| 13 | 223 | 0 | 0 | 0.969298 | 0.0114246 | 0.991951 | 0.947163 | (s0) |
| 15 | 221 | 0 | 0 | 0.964912 | 0.0121858 | 0.989094 | 0.941322 | (s0) |
| 26 | 220 | 0 | 0 | 0.960526 | 0.0128956 | 0.986137 | 0.935581 | (s0) |
| 30 | 219 | 0 | 0 | 0.95614 | 0.0135621 | 0.983094 | 0.929925 | (s0) |
| 31 | 218 | 0 | 0 | 0.951754 | 0.0141914 | 0.979979 | 0.924342 | (s0) |
| 53 | 217 | 0 | 0 | 0.942982 | 0.0153564 | 0.973566 | 0.91336 | (s0) |
| 54 | 215 | 0 | 0 | 0.938596 | 0.015899 | 0.970281 | 0.907947 | (s0) |
Similar to the survival the cumulative incidence table can be drawn as above. The obvious addition here is the presence of the prevalence column, indicating the cumulative prevalence of the outcome at each time point.
A pictorial overview of the cumulative incidence can also obtained using the commands below and shown in the figure below.
25.8 Comparing survival between two or more groups
It often arises that survival or hazard between two or more groups is compared. For instance in a randomised controlled trial to determine the survival in patients with a chronic disease 3 drugs can be given to three randomly selected groups. After a period of follow-up, one would want to compare which group survived best. To do this various non-parametric tests are available to help. Standing tall among them is the log-rank test (Peto et al, 1977) which we are going to apply.
25.8.1 The Log-Rank test
The idea behind the log-rank test is to test the proportional hazards among the groups to be compared. The test has a null hypothesis that the hazard is equal in all the populations under consideration. The p-value generated is the probability that the hazard is equal in all populations under consideration. Hence a small p-value indicates some differences exist at least between two members of the group. Below we use the log-rank test to determine if the hazards in the two sexes are significantly different for our lung cancer patients. Remember pictorially and by comparison of the median survival we already know that the females seem to do better than the males but here we put it to a formal test. This is done in R using survdiff() and the initial survival object created.
survdiff(Surv.1 ~ lung$sex)
Call:
survdiff(formula = Surv.1 ~ lung$sex)
N Observed Expected (O-E)^2/E (O-E)^2/V
lung$sex=Male 138 112 91.6 4.55 10.3
lung$sex=Female 90 53 73.4 5.68 10.3
Chisq= 10.3 on 1 degrees of freedom, p= 0.001 The small p-value above (p= 0.00131) leads us to the conclusion that the hazards within the two groups significantly differ.
25.8.2 Stratified Log-Rank test
In trying to figure out why females tend to do better than males with lung cancer we ask ourselves a few questions. One of these could be: Could it be because there is a difference in ages between the two sexes that took part in the study? To begin to evaluate this assertion we compare the ages of the two sexes.
lung %>%
group_by(sex) %>%
meantables::mean_table(.x=age)| response_var | group_var | group_cat | n | mean | sd | sem | lcl | ucl | min | max |
|---|---|---|---|---|---|---|---|---|---|---|
| age | sex | Male | 138 | 63.34 | 9.14 | 0.777983 | 61.8 | 64.88 | 39 | 82 |
| age | sex | Female | 90 | 61.08 | 8.85 | 0.932588 | 59.22 | 62.93 | 41 | 77 |
Well, it appears the males are on average older than the females. Could this be the reason why the males did worse? To remove the possibility of age being the reason why males may be doing worse we perform a stratified log-rank test below
survdiff(Surv.1 ~ lung$sex + strata(lung$age))
Call:
survdiff(formula = Surv.1 ~ lung$sex + strata(lung$age))
N Observed Expected (O-E)^2/E (O-E)^2/V
lung$sex=Male 138 112 96.6 2.47 9.42
lung$sex=Female 90 53 68.4 3.48 9.42
Chisq= 9.4 on 1 degrees of freedom, p= 0.002 The analysis above asks the question: Assuming the ages of all the sexes were equal among both sexes, would the survival still depend on the sex of the patient? After the analysis, it appears the age difference is not the reason for the difference in hazards observed. The significant p-value is hardly affected when we stratify by age.
25.9 Cox regression
Similar to our observation when we performed the chi-squared test in categorical data analysis, we only generated a p-value but no comparable effect like the odds ratio and risk ratio when we used the log-rank test. We cannot for instance say that the hazard in the males is twice that of the females. This is where Cox regression analysis kicks in. Cox regression analysis generates the Hazard Ratio (HR) a ratio similar to the odds ratio but this time compares the hazards in the various groups. Like the OR, HR has a null value of 1, when the hazard is equal in both groups being compared. Cox regression has the added advantage of being able to determine the HR for more than one variable at a time thereby correcting for their respective effects and stratifying at the same time. Cox proportional modelling is implemented in R using the function coxph(). Below we determine again the association between sex and the hazard in the lung data.
cox.1 <- coxph(Surv.1 ~ sex, data = lung)
cox.1 %>%
broom::tidy(exponentiate = TRUE, conf.int = TRUE)| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| sexFemale | 0.588003 | 0.167179 | -3.17638 | 0.00149123 | 0.423718 | 0.815985 |
Just like other regression functions in R, the output is scanty. However, the negative coeff indicated that the hazard is less in females compared to males (the referent group). Exponentiating the coefficient gives the hazard ratio. This is shown as the second column of the matrix with the heading exp(coef) and with a value of 0.588. This value indicates that females have about half the hazard of males. This is in concert with what we already know. The last column is the respective p-value associated with the coefficient or hazard ratio. It tests the hypothesis that the hazard ratio is equal to 1 (the null value). Therefore a small p-value makes this a significant finding. The last 2 columns are the confidence interval.
As was mentioned one of the advantages of using the Cox proportional regression is our ability to put in more than one variable at a time. Below we determine the hazard ratios for both sex and age concurrently and after correcting for each other.
cox.2 <- coxph(Surv.1 ~ sex + age, data = lung)
cox.2 %>%
broom::tidy(exponentiate = TRUE, conf.int = TRUE)| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| sexFemale | 0.598566 | 0.167458 | -3.06476 | 0.00217845 | 0.431094 | 0.831099 |
| age | 1.01719 | 0.00922327 | 1.84808 | 0.064591 | 0.998969 | 1.03575 |
And then finally we determine the HRs while stratifying for the ECOG performance score (0=good 5=dead)
cox.3 <- coxph(Surv.1 ~ sex + age + strata(ph.ecog), data = lung)
cox.3 %>%
broom::tidy(exponentiate = TRUE, conf.int = TRUE)| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| sexFemale | 0.574924 | 0.170873 | -3.23935 | 0.00119802 | 0.411304 | 0.803633 |
| age | 1.01083 | 0.0092538 | 1.16408 | 0.244392 | 0.992662 | 1.02933 |
Putting all three into one Cox’s regression equation we have the table below
lung %>%
select(sex, ph.ecog, age, status, time) %>%
survival::coxph(
survival::Surv(event = status==2, time = time) ~ .,
data = .) %>%
gtsummary::tbl_regression(
label = list(
age ~ "Age (years)",
sex ~ "Sex",
ph.ecog = "PH.ECOG"),
pvalue_fun = ~ gtsummary::style_pvalue(.x, digits = 3),
exponentiate = TRUE) %>%
gtsummary::bold_labels() %>%
gtsummary::bold_p()| Characteristic | HR1 | 95% CI1 | p-value |
|---|---|---|---|
| Sex | |||
| Male | — | — | |
| Female | 0.58 | 0.41, 0.80 | <0.001 |
| PH.ECOG | 1.59 | 1.27, 1.99 | <0.001 |
| Age (years) | 1.01 | 0.99, 1.03 | 0.232 |
| 1 HR = Hazard Ratio, CI = Confidence Interval | |||
Conclusion: It can be concluded that the hazards differ significantly between the two sexes, with females surviving better than males with lung cancer. Though the ages of the males in our study were relatively higher than the females this difference in age could not explain completely why males did worse than females. In other words, the difference in survival for the two sexes is irrespective of their age.