14 Analysis of categorical data
In this section we discuss how to analyse categorical data, both aggregated and non-aggregated.
14.1 One-sample binomial test
14.1.1 One sample proportion: Confidence interval
In a study to determine the prevalence of hypertension in a certain adult
population, a random sample taken revealed 23 out of 67 had hypertension. The
proportion of hypertensive patients in the sample is rather straightforward.
Approximately 0.34 or (34.3%) of the sample are hypertensives. We however
extrapolate to estimate this proportion in the population by estimating the
confidence interval. To do this single proportion estimation we use the
binom.test() function after we have fulfilled the conditions required for its
use. These are:
- The sample was obtained by simple random sampling
- There are just two possible outcomes for the data, here hypertension (successes) or no hypertension (failures).
- The sample includes at least 10 successes and 10 failures
- The population is at least 20 times larger than the sample size.
With our sample not violating these conditions, we go ahead to use the one-sample binomial test as below:
binom.test(23, 67) %>%
broom::tidy() %>%
select(-method)| estimate | statistic | p.value | parameter | conf.low | conf.high | alternative |
|---|---|---|---|---|---|---|
| 0.343 | 23 | 0.0139 | 67 | 0.232 | 0.469 | two.sided |
The binomial exact confidence interval of the proportion of those with hypertension in our study population, therefore, is 23.2% to 46.9%.
14.1.2 One sample proportion: Hypothesis testing
Before the data on hypertension above was collected, the investigator
hypothesized that 50% of the population was hypertensive. Next, we test this
hypothesis. As usual, we start by setting the null hypothesis.
H0: The population proportion of hypertensive in the population is 50%
binom.test(x=23, n=67, p=.5) %>%
broom::tidy()%>%
select(-method)| estimate | statistic | p.value | parameter | conf.low | conf.high | alternative |
|---|---|---|---|---|---|---|
| 0.343 | 23 | 0.0139 | 67 | 0.232 | 0.469 | two.sided |
It would be realised that this p-value is identical to that in the last
computation. This is because the binom.test() by default tests the proportion
against a 50:50 proportion in the population. At a 5% significance level, we
reject H0 and conclude the proportion of hypertensive in our population
significantly differs from 50%.
So, what if the investigators had hypothesized that prevalence in the population is 40%? Our null hypothesis would then have been:
H0: The population proportion of hypertensive is 40%
Next, we test this hypothesis.
binom.test(x=23, n=67, p=.4) %>%
broom::tidy()%>%
select(-method)| estimate | statistic | p.value | parameter | conf.low | conf.high | alternative |
|---|---|---|---|---|---|---|
| 0.343 | 23 | 0.384 | 67 | 0.232 | 0.469 | two.sided |
At a significance level of 0.05, we fail to reject the null hypothesis, concluding that there is insufficient evidence to conclude our population prevalence is not 40%.
Finally, what if the investigators had hypothesized that the population prevalence of hypertension is at least 47%? Remember this is a one-sided test and our null hypothesis would be
H0: The population proportion of hypertension is greater than or equal to 47%
And then we test the hypothesis
binom.test(23, 67, p=.47, alternative = "less") %>%
broom::tidy()%>%
select(-method)| estimate | statistic | p.value | parameter | conf.low | conf.high | alternative |
|---|---|---|---|---|---|---|
| 0.343 | 23 | 0.0244 | 67 | 0 | 0.45 | less |
The small p-value leads us to reject H0 and conclude it is insufficient evidence to support the assertion that the prevalence of hypertension in the population is at least 47%.
14.2 Two or more sample binomial test
14.2.1 Two sample proportion: Hypothesis testing
Taking it further we decide to select from a different population and sample 100
persons to determine the proportion of those with hypertension. In this
population, we came up with 52 hypertension patients out of a hundred. We aim to compare if there is a significant difference between the proportion of
hypertension patients in the two populations. To do this we use the
prop.test() function in R.
First, we state the null hypothesis: >H0: The population proportion of hypertension in both populations are the same.
Next, we test the hypothesis. To do this we first create two vectors representing the number of persons with hypertension and the total samples chosen.
hpt <-c(52, 23) # Vector of numbers with hypertension
n <- c(100, 67) # Vector of numbers in the sampleNext, we apply the test
| estimate1 | estimate2 | statistic | p.value | parameter | conf.low | conf.high | alternative |
|---|---|---|---|---|---|---|---|
| 0.52 | 0.343 | 4.37 | 0.0365 | 1 | 0.0142 | 0.339 | two.sided |
p-value of 0.0365 is less than our regular significance level of 0.05 so we reject the null hypothesis and say there is enough evidence to conclude that the prevalence of hypertension is not the same in the two populations.
The 95% confidence interval generated above is that of the difference between the two proportions, which is 0.177. The confidence interval of 0.014 to 0.339 does not include the null value 0 so we conclude that there is a difference in the prevalence of hypertension between the 2 populations.
14.3 Chi-squared test
Pearson’s chi-square test, also known as the chi-square goodness-of-fit test or chi-square test for independence is used to determine if observed frequencies in data are consistent with what is expected. For instance, in Asia, the percentages of ABO blood groups in the population are 38%, 10%, 3% and 49% for groups A, B, AB, and O respectively. In a random sample of 600 persons in Kumasi, Ghana 226, 82, 21 and 271 were blood groups A, B, AB, and O respectively. The chi-squared test can help us determine if the proportion of blood groups found in Kumasi is consistent with that seen in Asia.
14.3.1 Chi-squared goodness of fit test
In the blood group example above the investigators may want to know if the proportions of the blood groups in Kumasi are consistent with that seen in Asia. To do this we use the Chi-squared goodness of fit test. As always, we begin by making sure the test can be appropriately used under this condition. The assumptions of the test are:
- The data was obtained randomly from the population
- The variable under study is categorical
- Each of the observed values in each category is at least 5
With none of the conditions violated we go ahead to state the null hypothesis as
H0: The distribution of blood groups in Kumasi is not different from that in Asia.
Next, we perform the test but to do that we first create a data frame of the expected and observed frequencies in Asia and Kumasi respectively.
bld_grp <- c("A", "B", "AB", "O")
Asia <- c(38.0, 10.0, 3.0, 49.9)
Kumasi <- c(226, 82, 21, 271)
Kumasi <- round(Kumasi/sum(Kumasi)*100, 1)
df_temp <- data.frame(bld_grp, Asia, Kumasi)
df_temp| bld_grp | Asia | Kumasi |
|---|---|---|
| A | 38 | 37.7 |
| B | 10 | 13.7 |
| AB | 3 | 3.5 |
| O | 49.9 | 45.2 |
Next, we illustrate these proportions using a barplot by plotting the same blood groups from different regions side by side.
df_temp %>%
pivot_longer(
cols = c(Asia, Kumasi),
names_to = "Place",
values_to = "Perc") %>%
mutate(
labels = paste(
format(round(Perc,1), nsmall=1), "%", sep="")) %>%
ggplot(aes(x = bld_grp, y = Perc, fill = Place)) +
geom_bar(stat="identity", position= position_dodge()) +
geom_text(
aes(label=labels), vjust=1.5, color="black",
size=3.5, position = position_dodge(0.9)) +
scale_fill_brewer(palette="Blues") +
labs(
title="Comparative distribution of Blood Groups",
x = "Blood Group",
y = "Frequency")+
theme_bw()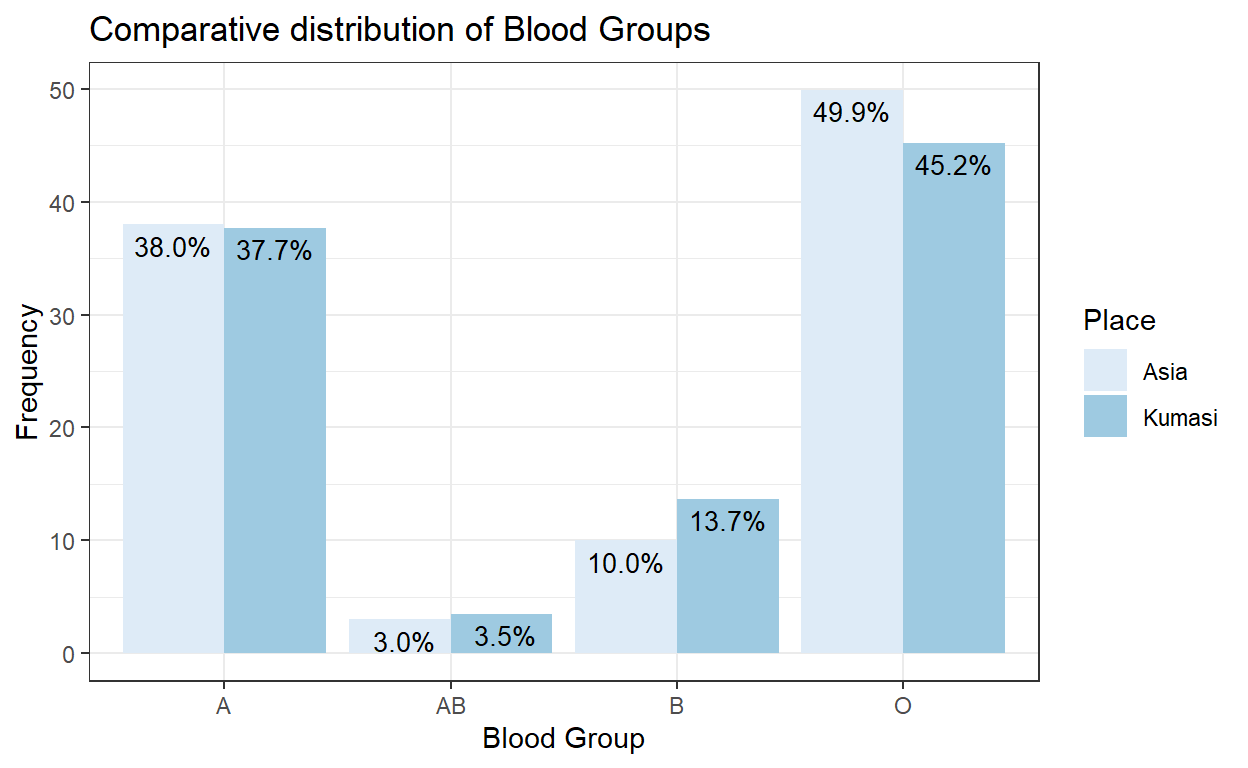
We observe the similarities between the proportions from Kumasi and Asia. For instance, the blood groups from both regions show decreasing frequency from O, A, B and AB. However, we also observe that adjacent bars are not exactly of the same height. Blood groups O and B for instance have approximately a 4%-point difference between the two populations. Next, we perform the actual test for the difference in proportions.
chisq.test(x = Kumasi, p = Asia/sum(Asia)) %>%
broom::tidy()
Warning in chisq.test(x = Kumasi, p = Asia/sum(Asia)):
Chi-squared approximation may be incorrect| statistic | p.value | parameter | method |
|---|---|---|---|
| 1.91 | 0.592 | 3 | Chi-squared test for given probabilities |
With a p-value of 0.592, we fail to reject H0 and conclude there is no evidence that the proportions of blood groups in Kumasi are different from the observed proportions in Asia.
14.3.2 Chi-squared test for independent data
In this subsection, we will use the ANCdata from the epicalc package. It can also
be obtained from the list of data that comes with this book. The ANCdata
contains records of high-risk pregnant women in a trial to compare a new and an
old method of antenatal care (anc) in two clinics (clinic). The outcome was
perinatal mortality, the death of the baby within the first week of life (death).
We begin by loading the ANCdata
df_anc <-
read.delim("./Data/ANCData.txt") %>%
mutate(
death = factor(death, levels = c("no","yes"), labels = c("No", "Yes")),
clinic = factor(clinic),
anc = factor(anc, levels = c("old", "new"), labels = c("Old", "New")))
df_anc %>% summarytools::dfSummary(graph.col = FALSE)
Data Frame Summary
df_anc
Dimensions: 755 x 3
Duplicates: 747
--------------------------------------------------------------------------
No Variable Stats / Values Freqs (% of Valid) Valid Missing
---- ---------- ---------------- -------------------- ---------- ---------
1 death 1. No 689 (91.3%) 755 0
[factor] 2. Yes 66 ( 8.7%) (100.0%) (0.0%)
2 anc 1. Old 419 (55.5%) 755 0
[factor] 2. New 336 (44.5%) (100.0%) (0.0%)
3 clinic 1. A 497 (65.8%) 755 0
[factor] 2. B 258 (34.2%) (100.0%) (0.0%)
--------------------------------------------------------------------------Our objective in this section is to determine if there is a significant relationship between the anc type and perinatal death. In other words, does perinatal mortality differ in the population depending on the anc method used?
To begin we cross-tabulate the two variables.
df_anc %>%
tbl_cross(percent = "col",
row = death,
col = anc,
label = list(death ~ "Death", anc = "ANC")) %>%
bold_labels()| ANC | Total | ||
|---|---|---|---|
| Old | New | ||
| Death | |||
| No | 373 (89%) | 316 (94%) | 689 (91%) |
| Yes | 46 (11%) | 20 (6.0%) | 66 (8.7%) |
| Total | 419 (100%) | 336 (100%) | 755 (100%) |
df_anc %>%
group_by(death, anc) %>%
count() %>%
ggplot(aes(fill = death, y = n, x = anc)) +
geom_bar(position = "fill", stat = "identity", col = "black") +
scale_fill_discrete(name = "Death", type = c("white","red"))+
labs(
y = "Proportion",
x = "ANC Type",
title = "Distribution of the ANC method used and perinatal deaths") +
theme_bw()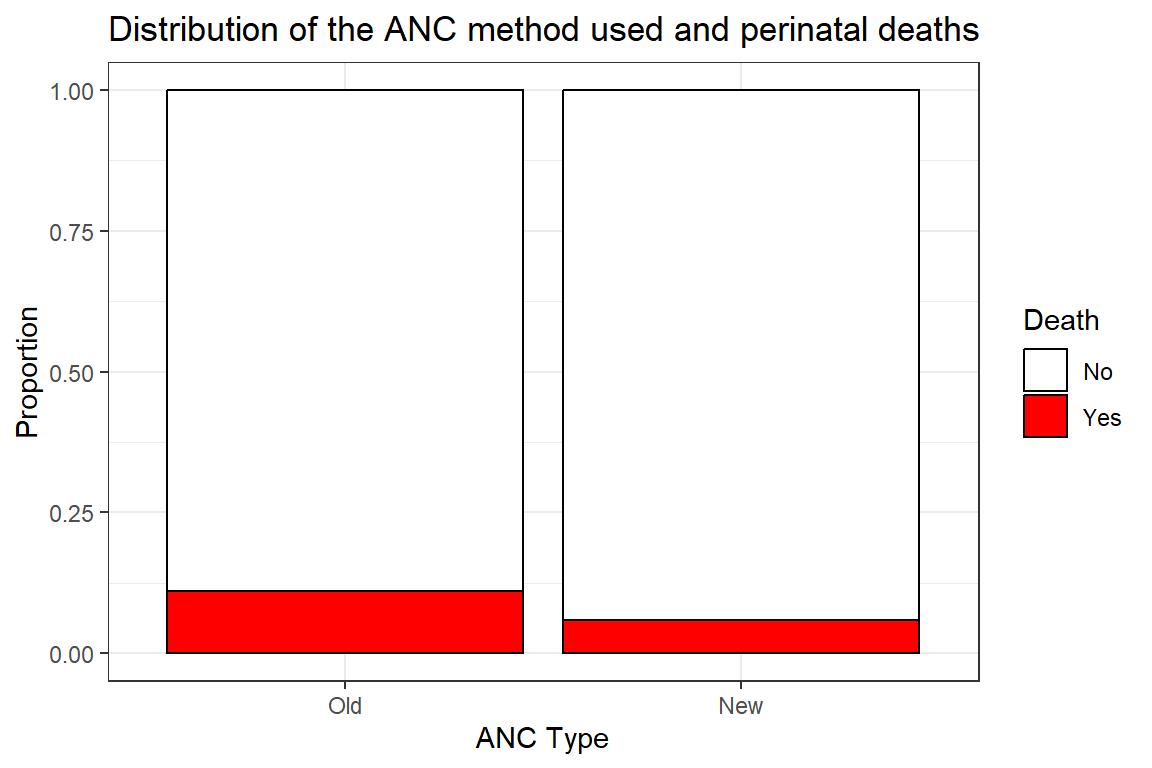
The cell proportions are not uniform. The proportion of deaths in those who used the old and anc methods is about 11.0% and 5.9% respectively. Is this enough evidence to conclude the new is better than the old in the population? This question we would have to answer using a formal statistical test.
Test for independence for tabular data often entails the use of the Chi-squared test and/or Fisher’s exact test. Independence here simply means when one has one variable one cannot predict the other variable.
Next, we apply the chi-squared test after we have verified that our data does not violate the assumption required for its use. These are.
- The data was obtained randomly from the population
- The variables under study are categorical
- Each observation fits into only one cell of the table
- The expected values in each cell of the tabular data are at least 5
Our data does not violate any of these so we go ahead to state the null hypothesis.
H0: There is no difference in the proportion of perinatal deaths between mothers who used the new and old ANC methods.
And perform the test
df_anc %$%
table(anc, death) %>%
chisq.test() %>%
broom::tidy()| statistic | p.value | parameter | method |
|---|---|---|---|
| 5.29 | 0.0214 | 1 | Pearson's Chi-squared test with Yates' continuity correction |
The test above yields a relatively small p-value compared to a significance level of 0.05, indicating the null hypothesis of independence of the cell proportions are unlikely. In other words, the cell proportions differ significantly, the old method can be said to result in significantly higher perinatal deaths compared to the new method.
14.3.3 Chi-squared test for trend
Often there arise situations in categorical data analysis where the objective is not to just see a difference in proportions as a Chi-squared test for independence or Fisher’s test does but to determine any trend in the proportions seen. Here the Chi-squared test for trend is often employed.
For example, in a study to determine the proportion of persons having eye changes the following data was obtained: 4 out of 42 persons aged less than 45yrs, 7 out of 43 aged between 46yrs and 55yrs, 12 out of 46 aged between 56yrs and 65yrs and 15 out of 44 aged more than 65yrs. First, we input these into R and calculate the percentages with the eye changes.
Next, we determine the percentage of those with eye changes for each age group
Perc.eye<-round(No.eye/No.studied * 100, 1)Next, we form a matrix showing the number of persons with eye changes, the number of persons studied and the percentage of persons with eye changes for each age group.
names(No.eye)<-c("<=45yrs","46-55yrs","56-65yrs",">65yrs")
cbind(No.eye, No.studied, Perc.eye)
No.eye No.studied Perc.eye
<=45yrs 4 42 9.5
46-55yrs 7 43 16.3
56-65yrs 12 46 26.1
>65yrs 15 44 34.1From the analysis above it can be said that the proportions of persons with eye changes increases with age. However, to determine if this apparent rise could be a chance finding we apply the Chi-Squared test after we confirm the data does not violate the assumptions for its use. The condition for its use is like the chi-squared test for independent data but with an addition that at least one of the variables must be ordered. Now satisfied that our data satisfies the conditions we state the null hypothesis.
H0: There is no trend in the eye changes with increasing age
Next, we put it to the formal test
prop.trend.test(No.eye, No.studied) %>%
broom::tidy()| statistic | p.value | parameter | method |
|---|---|---|---|
| 8.86 | 0.00291 | 1 | Chi-squared Test for Trend in Proportions |
With a p-value less than 0.05, we reject the H0 and conclude that there a significant trend (upward because we know it is) in developing eye changes with increasing age.
14.4 Fisher’s Exact test
A valid conclusion from the use of the chi-squared test can only be guaranteed if the counts in all the cells of the table in question are equal to or greater than 5. Whenever the count or value in any of the cells is below 5, Fisher’s exact test must be used instead. Its use and interpretation are similar to the chi-squared test and are demonstrated with the ANCdata as below.
df_anc %$%
table(anc, death) %>%
fisher.test() %>%
broom::tidy()| estimate | p.value | conf.low | conf.high | method | alternative |
|---|---|---|---|---|---|
| 0.514 | 0.0191 | 0.282 | 0.908 | Fisher's Exact Test for Count Data | two.sided |
The p-value here is quite like that obtained by the chi-squared test but not the
same. However, the conclusion remains the same. The added advantage of using
fisher.test() is the provision of the odds ratio and its 95% confidence
interval. The odds ratio will be explained in subsequent sections.